数字推理题所涉及的数字规律千变万化,对于数字推理题没有万能的解法,专家建议考生应重点分析题干数字的运算关系和位置关系。这就要求考生掌握相关的基础数学知识,还要掌握一定的解题方法,提高解题速度。
一、四大解题思维方法
(一)直觉思维
直觉思维是对事物直观认识的特殊思维方式,是逻辑思维的凝结或简缩。它包括数字直觉和运算直觉两个方面。
1.数字直觉
数字直觉是人们对数字基本属性深入了解之后形成的。通过数字直觉解决数字推理问题的实质是灵活运用数字的基本属性。
自然数平方数列:4,1,0,1,4,9,16,25, ……
自然数立方数列:-8,-1,0,1,8,27,64, ……
质数数列: 2,3,5,7,11,13,17,……
合数数列: 4,6,8,9,10,12,14,……
2.运算直觉
运算直觉是对数字之间的运算关系熟练掌握之后形成的。通过运算直觉解决数字推理问题的实质是灵活运用数字之间的运算关系。

数字直觉侧重于一个数本身的特性,运算直觉则侧重于几个数之间的关系。数字直觉和运算直觉是数字推理直觉思维中不可分割的两部分,解题时需综合运用这两种直觉思维。
(二)构造思维
构造思维是从已知条件出发,建立新的分析模式,最终解决问题的思维模式。
在解决数字推理问题时,构造的方法通常有基本数列构造、作差构造、作商构造、作和构造和作积构造,通过构造新的数列,将复杂的数列转化为容易发现规律的简单数列。

(三)转化思维
从各类公务员考试的真题来看,数列前面的项按规律转化得到后面的项是十分常见的梳理推理规律。转化思想就是在解题过程中有意识的去寻找这种转化方式。
例题:4 ,4 ,9 ,29 ,119 ,( )
A.596 B.597 C.598 D.599
解析:前面几项的比值近似整数,提示我们数字推理规律可能与倍数有关,由4到9的转化方式应是4×2+1=9,由9至29的转化转化方式应是9×3+2=29;可以看出倍数分别是2、3。加数分别是1、2,由此可知:4×1+0=4、29×4+3=119、119×5+4=(599)。
(四)综合思维
由于题干数字的迷惑性,数字推理规律隐藏得很深,解题时可能是直觉思维、构造思维、转化思维交替运用的过程,是猜证结合的过程,这就是一种综合思维。
当前数字推理规律求新求异,真题中时有“出人意外”的数字推理规律出现,这就要求我们在掌握一些基本解题方法的基础上,结合对数字推理规律的积累,多角度开阔思路,实现数字推理解题能力的全面提升。
下面,专家结合实例,重点介绍一下在解数字推理的过程中,常见的一些解题思路。
二、解题思路
1.当数列呈递增或递减趋势,且变化幅度不大时,优先使用作差法。

另外,当数列中无明显规律,寻找数项特征和结构特征也没有头绪时,也可以考虑使用作差法理清关系。
2.当数字之间存在明显倍数关系时,应优先应考虑使用作商法。
例题:4,7,15,29,59,( )
A.68 B.83 C.96 D.117
解析:初看相邻项的商约为2,再仔细观察,不难发现,4×2-1=7,7×2+1=15,……。故此题答案为59×2-1=(117)。
3.当数列各项的跳跃性较大时,则应考虑多次方、相邻项相乘等关系。
例题:3,4,6,12,36,( )
A.8 B.72 C.108 D.216
解析:此题考察数列的积数列变式,A×B/2=C,即有36×12/2=(216)。故此题答案为D 。
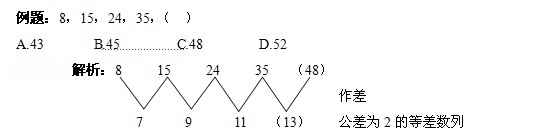
4.数列有平稳、递增趋势,但通过作差不能解决问题,利用多次方和作商也不能解决时,可考虑取两项或三项求和,从而寻找新数列的规律。
5.拆分法的应用,拆分法是指将数列中的数字拆分成两个或多个部分,然后通过每部分的规律得到原数列规律的方法,在公务员考试中,拆分法主要有整数乘积拆分与整数加减拆分两种。
例题:87,57,36,19,( )
A.12 B.11 C.10 D.9
解析:乍看没有规律,仔细观察会发现第二项57=8×7+1,后面各项也遵循此规律,故1×9+1=(10)。所以正确答案为C。
6.当数列的项数很多时,可以首先考虑分组,观察两个一组(或三个一组)及隔项之间是否有规律等。
例题:4,3,1,12,9,3,17,5,( )
A.10 B.12 C.13 D.15
解析:此题项数很多,故应首先考虑分组法,三项一组,第一项=第二项+第三项,依此类推,17=5+(12).故答案为B。
7.分式数列在公务员考试中比较常见,其题干一般由一系列分数组成,大多与其他数列综合起来考查。解此类题型的主要思维是将题干分数进行合理的通分和改写(一般化为质数列、等差、等比数列等)。

行测更多解题思路和解题技巧,可参看2012年公务员考试技巧手册。









