几何知识在现实中有着广泛应用，政法干警行测考试中的几何问题将越来越倾向于将考点与现实问题结合考查。几何是衡量空间的数学分支，“几”在文言文中表示：衡量大小。点--线--面--空间的几何学研究路线也是从低维到高维，简单到复杂的过程。因此，浙江公务员考试网（http://www.zjgwy.org）建议各位考生，在几何问题中秉着类似“大事化小小事化了”的原则将复杂问题简单化，反而更利于考试作答。下面以实例说明。

　　【例题１】 单个通信基站的信号覆盖区域有限，是一个以基站为圆心半径固定的圆形。考虑基站位置如何分布以使信号全面覆盖某市时，通常把该市划分成一个个面积相同可无缝拼接的正多边形单元，单个基站信号覆盖区域即这个正多边形的外接圆。那么正多边形边数为多少时，所需基站数量最少？

　　Ａ．３                                   Ｂ．４                                Ｃ．６                                Ｄ．８

　　【解析】该市总面积一定，基站的数量取决于正多边形的数量。因此，基站信号所覆盖的圆的内接正多边形面积越大，正多边形小单元数量越少，所需基站数量也就越少。同时，要令正多边形无缝拼接，只有当边数为３、４、６时才能满足。综上，基站呈六边形蜂窝状分布时，需要设置的基站数量最少，选Ｃ。

　　【例题2】 为了浇灌一个半径为１０米的花坛，园艺师要在花坛里布置若干个旋转喷头，但库房里只有浇灌半径为５米的喷头，问花坛里至少要布置几个这样的喷头才能保证每个角落都能浇灌到？

　　Ａ．４                                   Ｂ．７                                Ｃ．６                                Ｄ．９

　　【解析】已知花坛是半径为１０米的大圆，喷头是半径为５米的小圆，此题转化为求“多少个半径为５的小圆可以完全覆盖半径为１０的大圆？”。把小圆理解为“基站”，当这些基站呈蜂窝状排列时实现无缝隙覆盖用到的“基站”数量最少。如图所示，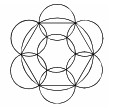

　　至少要７个小圆蜂窝状排列能够实现对大圆无缝隙的完全覆盖。

　　【例题3】 把一个正四面体的每个表面都分成９个相同的等边三角形，用任意颜色给这些小三角形上色，要求有公共边的小三角形颜色不同，问最多有多少个小三角形颜色相同？

　　Ａ．１２                         Ｂ．１５                     Ｃ．１６                     Ｄ．１８

　　【解析】设颜色相同最多的为黑色；与黑色小三角形异色的三角形暂用白色标记。

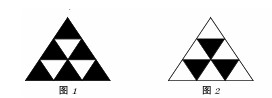
　　任取一个面，其中黑色的三角形最多为６个（如图１）。这种情况下，其他３个面每个面最多有３个黑色小三角形（如图２）。最多有６＋３×３＝１５个黑色小三角形，选Ｂ。

　　【例题4】 一条路上依次有Ａ、Ｂ、Ｃ三个站点，加油站Ｍ恰好位于ＡＣ的中点，加油站Ｎ恰好位于ＢＣ的中点。若想知道Ｍ和Ｎ两个加油站之间的距离，只需要知道哪两点之间的距离？

　　Ａ．ＣＮ                         Ｂ．ＢＣ                            Ｃ．ＡＭ                            Ｄ．ＡＢ

　　【解析】从的命题分析来看，命题人通过这样一个文字应用题考查的是应试者的理解能力，核心是要用图来描述题中点的位置关系，将文字转化为图形。

　　浙江公务员考试网建议考生穿越题海找规律,做题速度快,效率高,取得好成绩近在咫尺!

　　行测更多解题思路和解题技巧，可参看2014年公务员考试技巧手册。