1.计算:(2＋4＋6＋8＋…＋2010)－(1＋3＋5＋7＋…＋2009)＝(  )。
      A.995              B.1011              C.1111               D.1005

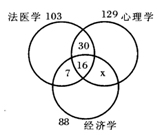
      2.法学院200名学生,每人至少辅修法医学、心理学和经济学三项中的一项。其中,辅修法医学的学生有103人,辅修心理学的学生有129人,辅修经济学的有88人。三科全都选择的有16人。只选择法医学和心理学的有30人,只选择法医学和经济学的有7人,那么只选择心理学和经济学的学生有(  )人。
　　A.51               B.35                C.67                 D.83

      3.5人参加一次小测验,试卷上的10道题目均为4选1的单项选择题,若5个人全部答完所有题目,那么不同的答卷最多有(  )种。
　    A.410                       B.510                       C.40                 D.200

      4.袋子里装有红、蓝两色的小球各12个,先从袋子中拿出一个球,然后将它放回袋子中,混合后再从中拿出一个小球。那么两次抽中不同颜色的小球的几率有(  )。
　　A.20%              B.25%              C.50%               D.60%

      5.一堆棋子,排成一个方阵后多余出5枚棋子,若在这个方阵纵横两个方向各增加一层,则缺少10枚棋子。那么这堆棋子共有多少枚?(  )
      A.54枚             B.44枚             C.41枚               D.31枚

      （浙江公务员网http://www.zjgwy.org）参考答案解析

      1.D【解析】原式＝(2－1)＋(4－3)＋(6－5)＋(8－7)＋…＋(2010－2009)
　　　　　　　　    ＝1＋1＋1＋1＋…＋1
　　从2到2010共有1005个偶数,所以原式等于1005个1相加,等于1005,故本题答案为D。

      2.A【解析】设只选择心理学和经济学的学生人数为x,根据题干要求画出关系图,通过观察可列出等式:103＋129＋88－30－7－x－l6×2＝200,解得x＝51,即有51人只选择辅修心理学和经济学。答案为A。
 

　　3.A【解析】从第1题开始最多可能出现4种不同的答案,然后在做第2题时也可能有4种不同的答案,直到第10题依然会出现4种答案。符合排列组合中乘法原理,因此不同的答卷一共会出现:4×4×4×…×4＝410(种)。故答案为A。

　　4.C【解析】因为两种颜色的小球数量相等,那么每次抽中其中一种颜色小球的概率均为50%。第一种情况:第一次抽中了红色小球,第二次抽中了蓝色小球,概率是50%×50%一25%;第二种情况:第一次抽中了蓝色小球,第二次抽中了红色小球,概率是50%×50%＝25%。那么两次抽中不同颜色的小球的整体概率等于两种情况下的概率之和,即25%＋25%＝50%,答案为C。

　　5.A【解析】设原方阵每边有棋子x枚,根据题意可知:x2＋5＝(x＋l)2－10,解得x＝7,那么这堆棋子的数量为:7×7＋5＝54(枚)。答案为A。