距离浙江省仅剩20余天时间，随着考试时间的临近，备考的时间也越来越紧张，针对于省考历年考情，今天详细去带大家了解一下关于省考中最让考生们头大的重点题型：资料分析和数量关系。这两个模块在整个行测试卷当中分值占比较大，尤其数量关系一直以来都是大家丢分最严重，最不容易拿分的模块，但是想要进面必须不能放弃这模块。因此，学好这两个模块，尤为重要，甚至是考高分的关键。

　　

　　资料分析其实非常简单，为什么呢？

　　一、考点较少

　　大多数题目是围绕7个核心考点来出题的，分别是基期值，现期值，增长量，增长率，倍数，比重，平均数。

　　二、题型固定

　　资料分析做题比较套路化，大多数题目做题步骤是找数据---列公式---计算。资料分析单个题目的分值较大，在1分左右。因此资料分析比较好拿分，掌握不好也很容易拉分，至关重要。

　　（一）增长相关

　　1.基本公式

　　

　　2.出题标志

　　基期量的出题标志：基期时间+主语

　　现期量的出题标志：如果明年保持同样增速

　　增长量的出题标志：增加了/增加/增产...+量的单位

　　增长率的出题标志：增加了/增加/增速为...+a%

　　3.计算技巧

　　(1)化除为乘法

　　适用题型：已知现期量和增长率,计算基期量。（范围：∣a%∣≤10%）

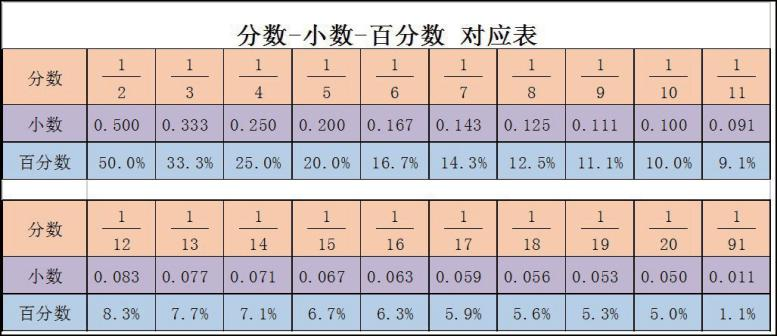
　　(2)特征数字法

　　适用题型：已知现期量和增长率,计算增长量.

　　增长量=现期量/(N+1)   减少量=现期量/(N-1)     (a%=1/N, a%表示增长率)

　　

　　【例1】2017年的产量是678.12吨，较2016年下降3.27%，问2016年的产量约是多少吨？

　　A.658     B.600    C.700     D.800

　　【答案】C

　　【解析】第一步，本题考查基期问题。

　　第二步，材料已知现期量和增长率求基期量，基期量=现期量/(1+增长率)=678.12/(1-3,27%)≈680×(1+3%)≈700.

　　因此，选择C。

　　【例2】2009 年世界天然气贸易量达8768.5亿立方米，较2005年增长7.7%。其中俄罗斯是世界最大的管道天然气出口国，占管道天然气总出口量的27.8%，出口量为1764.8亿立方米，较2008年增长14.3%。

　　问2009年俄罗斯管道天然气出口较上年增长了多少亿立方米？（  ）

　　A.110     B.221   C.332     D.443

　　【答案】B

　　【解析】第一步，本题考查增长量问题。

　　第二步，根据题干“增长了多少亿立方米”，可判定本题考查增长量问题。材料已知现期量和增长率求增长量。由于14.3%=1/7，增长量=现期量/(N+1)=1764.8/(7+1)，首位商2。

　　因此，选择B。

　　（二）隔年相关

　　隔年增长率：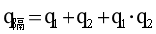

　　隔年基期量：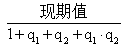

　　
　　（三）倍数相关

　　1.基本公式：

 

　　注意

　　(1)看清楚题目问得是“A是B的多少倍”还是“A比B多多少倍”,多多少倍不要忘记减1。

　　(2)看清楚时间,问得是基期倍数还是现期倍数。

　　【例1】

　　

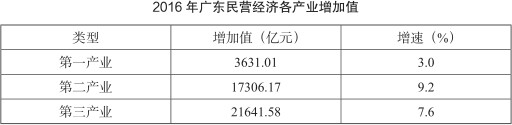
　　2016 年广东民营经济第二产业实现的增加值比第一产业大约多多少倍？（   ）

　　A.3.8     B.4.8    C.5.8      D.6.8

　　【答案】A

　　【解析】第一步，本题考查倍数问题。

　　第二步，根据题干所求“2016年广东民营······多多少倍”，且材料数据为2016年，可判定此题为现期倍数问题。定位表格，民营经济第一产业、第二产业增加值分别为3631.01亿元、17306.17亿元，17306.17÷3631.01-1≈3.8.

　　因此，选择A。

　　（四）比重相关

　　1.基本公式：

　　现期比重：

　　基期比重：

　　判断比重变化：

　　

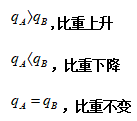
　　比重增长量：

　　2.解题技巧

　　(1)现期比重

　　出题标志：现期时间+占；

　　注意：比重的整体必须包含部分。

　　(2)判断比重变化

　　出题标志：“部分”占“整体”的比重高于/低于上年同期水平。

　　判断比重变化的步骤：①列式子 ②抄数据 ③画箭头。

　　(3)比重增长量

　　出题标志：“部分”占“整体”的比重比上年上升/下降____个百分点。

　　求比重增长量的步骤：①列式子 ②抄数据 ③画箭头 ④选小数。

　　唯一选它，不唯一计算。

　　(4)基期比重

　　出题标志：基期时间+占。

　　【例1】

　　某市2013年1~3月规模以上文化创意产业情况

　　

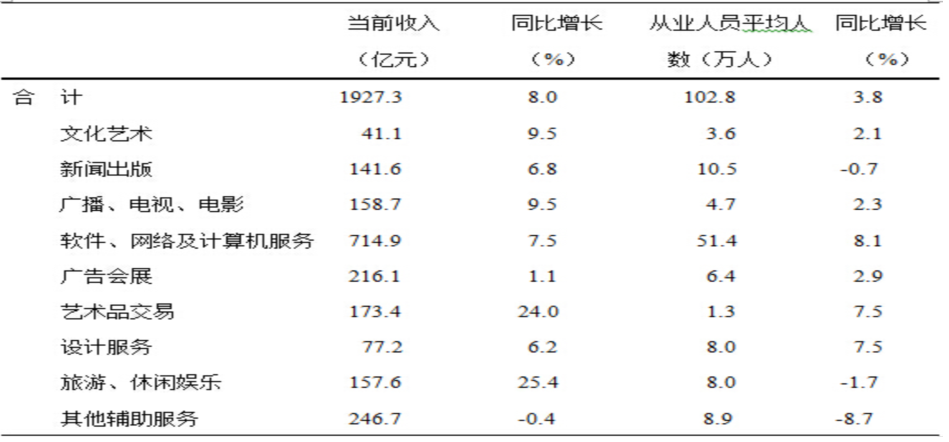
　　2013年第一季度，该市软件、网络及计算机服务行业从业人员平均人数占整个规模以上文化创意产业的比重比上年同期？（）

　　A.下降了4.3个百分点

　　B.上升了2个百分点

　　C.上升了4.3个百分点

　　D.下降了2个百分点

　　【答案】B

　　【解析】第一步，本题考查比重增长量。

　　第二步，由题干“2013年第一季度···占···比重比上年同期”，判定此题考查比重增长量。1.列式子;根据问题所列式子为:软件、网络及计算机服务行业从业人员平均人数/整个规模以上文化创意产业; 2.抄数据:定位表格可知2013年第一季度软件、网络及计算机服务行业从业人员平均人数A=51.4万人，同比增长率为qA=8.1%；整个产业从业人员平均人数B=102.8万人，同比增长率为qB=3.8%;3.画箭头: 部分增长率8.1%大于整体增长率3.8%,箭头向上,表示上升,排除A,D.4.选小数:|8.1%-3.8%|=4.3个百分点,选项里只有B小于4.3个百分点.

　　因此，选择B。

　　（五）平均数相关

　　1.基本公式

　　现期平均数：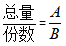

　　基期平均数：

　　平均数增长量：

　　平均数增长率：

　　注意:平均数增长率公式里分母是1+qB

　　2.出题标志

　　现期平均数：现期时间+平均、每；

　　基期平均数：基期时间+平均、每；

　　平均数增长量：平均/每+增长了+单位；

　　平均数增长率：平均/每+增长了+x%；

　　【例1】2017 年上半年，S 市出口手机 1.9 亿台，比去年同期减少 22.7%；价值 513.1 亿元人民币，下降 23.7%。6 月份当月出口 3217.5 万台，减少 23.7%；价值 86 亿元，下降 27.8%。

　　2017 年上半年，S 市平均每台出口手机的价值比去年同期约（ ）。

　　A.上升 0.8% B.上升 1.3%

　　C.下降 0.8% D.下降 1.3%

　　【答案】D

　　【解析】第一步，本题考查平均数增长率。

　　第二步，由题干“平均每台出口手机的价值比去年同期约”，选项里面给的是上升或下降的百分数，可判定本题为平均数增长率计算问题。平均每台出口手机的价值=，根据平均数增长率=代入数据，定位材料第一段，qA为价值的增长率是-23.7%，  qB为出口台数的增长率是-22.7%，平均数增长率==，所以下降超过1%，只有D满足.

　　因此，选择D。

　　（五）混合增长率相关

　　1.出题标志

　　量A+量B=量C,

　　2.口诀

　　居中不正中，偏向量（基期量）大的

　　【例1】2013 年 3 月末，地产开发贷款余额 1.04 万亿元，同比增长 21.4%。房产开发贷款余额 3.2 万亿元，同比增长 12.3%。

　　【问】2013 年 3 月末，房地产开发余额同比增速为？（  ）

　　A.14.4%   B.12.3%   C.19.3%   D.21.4%

　　【答案】A

　　【解析】第一步，本题考查混合增长率。

　　第二步，题干所求为2013年3月末房地产开发贷款余额同比增速，可知本题为一般增长率的计算问题。由材料知,地产开发贷款余额为1.04万亿元，同比增长21.4%。房产开发贷款余额为3.2万亿元，同比增长12.3%。地产余额+房产余额=房地产开发贷款余额，则房地产同比增速为地产与房产的混合增长率。根据混合增长率特点，所求混合增长率一定介于12.3%与21.4%之间，排除B、D两项。且偏向基期量较大的一侧，估算可知，房产的基期量大于地产基期量，偏向12.3%一侧。

　　因此，选择A。

　　

　　浙江省考的考试中数量关系以统筹问题、利润问题、容斥问题、周期问题等为测查重点，但题目难度并不高，多为简单计算，接下来让我们一起看看下列真题，你是否可以在兼顾速度和正确率的前提下逐一击破呢！

　　（一）两者相斥

　　容斥问题是利用集合间关系进行计数的数量问题，其中两者容斥是命题人偏爱的考点之一，2018年考察2道。在这个考点下，一是需要掌握公式：I=A+B+Y-A∩B，二是需要学会画文氏图：

　　

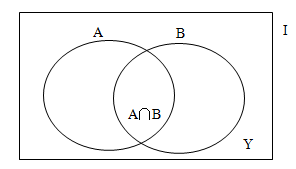
　　【例1】一个停车场有 50 辆汽车，其中红色轿车 35 辆，夏利轿车 28 辆，既不是红色轿车又不是夏利轿车 8 辆，问停车场有红色夏利轿车多少辆？

　　A.14 辆    B.21 辆   C.15 辆   D.22 辆

　　【答案】B

　　【解析】二者容斥问题。设红色夏利 x 辆，代入两集合容斥的公式：35+28-x+8=50，解得x=21，故本题选择 B 选项。

　　例：某职业大学的 750 名学生或上计算机课，或上规划设计课，或两门都上。如果有 489 名学生上计算机课，606 名学生上规划设计课，问两门都上的学生是多少？

　　A.118 人  B.114 人  C.261 人  D.345 人

　　【答案】D

　　【解析】二者容斥问题。设两门都上的人数为 x，代入两集合容斥的公式：489+606-x=750，解得 x=345，故本题选择 D 选项。

　　（二）利润问题

　　在解决利润问题之前，我们必须打好基础，掌握利润问题的常考公式：

　　关于利润：

　　利润 = 售价－成本 = 成本 × 利润率

　　利润率= 利润 / 成本 = （售价 - 成本） / 成本 = 售价 / 成本 - 1

　　成本 = 售价－利润 = 利润 / 利润率 = 售价 / （1 + 利润率）

　　售价= 成本+利润 = 成本×（1+利润率）

　　关于打折：

　　打折率 = 售价 / 定价

　　定价 = 售价 / 打折率

　　售价 = 定价 × 打折率

　　【例】老王两年前投资的一套艺术品市价上涨了50%，为尽快出手，老王将该艺术品按市价的八折出售，扣除成交价5%的交易费用后，发现与买进时相比赚了7万元。问老王买进该艺术品花了多少万元?

　　A.42     B.50   C.84    D.100

　　【答案】B

　　【解析】简单利润问题，直接设成本为X，根据题干中等量关系可以列出方程，1.5X·0.8(1-5%)-X=7， 解方程求得X=50。

　　即该艺术品的成本为50万元。答案选B。

　　（三）工程问题

　　核心公式：工作总量=工作效率×工作时间

　　赋值法：

　　①已知若干个工作时间，赋值总量为工作时间的公倍数；

　　②已知效率之间的比例关系，按比例赋值效率。

　　③N个相同的人/机器，赋值每人的效率为1；总量和效率均不好赋值时，设总量为单位1，把效率设为未知数，列方程求解。

　　【例1】一项工程，甲一人做完需30天，甲、乙合作完成需18天，乙、丙合作完成需15天，甲、乙、丙三人共同完成该工程需：（    ）

　　A．10天     B．12天    C．8天    D．9天

　　【答案】A

　　【解析】通篇给定时间，赋值工作总量为时间的最小公倍数90，可得：甲=3，乙+丙=6，故三人合作完成该工程需要10天。

　　【例2】一项工程，甲、乙合作12天完成，乙、丙合作9天，丙、丁合作12天完成。如果甲、丁合作，则完成这项工程需要的天数是？（    ）

　　A．16      B．18     C．24    D．26

　　【答案】B

　　【解析】通篇给定时间，赋值工作总量为时间的最小公倍数36，可得：甲+乙=3，乙+丙=4，丙+丁=3。可得：甲+丁=2，则两人合作完成此项工程需要18天。

　　（四）构造数列

　　题型识别：

　　N件物品分成M项，求其中某一项的最值（最大值或最小值）。

　　解题思路：

　　①编号：分成几项即依次编号为①②③④……

　　②求谁设谁；

　　③按照题目要求完成构造、利用总和为定值列方程求解。

　　【例1】要把21棵桃树栽到街心公园里5处面积不同的草坪上，如果要求每块草坪必须有树且所栽棵数要依据面积大小各不相同，面积最大的草坪上至少要栽几棵？（    ）

　　A．7   B．8   C．10   D．11

　　【答案】A

　　【解析】设面积最大的草坪上至少要栽x棵，则第二大、第三大......面积依次为（x-1）、（x-2）、（x-3）、（x-4），列出等式:x+（x-1）+（x-2）+（x-3）+（x-4）=21,解得x=6余1棵，所以至少种植7棵。

　　通过以上知识点和例题，应该也对这两个模块有了一定的认识，确实是有一定的难度，并且可能会很浪费时间，甚至影响到考试的心态。所以，一定要正确去看待这一部分题型，要做到有所取舍。

　　同样的也希望各位同学在备考中不要轻易去放弃这一部分内容的学习。最后，希望本篇能在大家最后冲刺阶段带来一定的帮助。祝大家笔试顺利进面，成功上岸！